مقدمهای بر معادلات فلومتر کوریولیس
فلومترهای کوریولیس (Coriolis Flowmeter) بهدلیل دقت بینظیر و عملکرد پایدار، از جمله پیشرفتهترین ابزارهای اندازهگیری دبی جرمی در صنایع مختلف به شمار میروند. برخلاف فلومترهای حجمی که حجم سیال را اندازهگیری میکنند، اساس عملکرد فلومتر کوریولیس بر پایهی پدیدهی فیزیکی شتاب کوریولیس بنا شده است. این شتاب زمانی بهوجود میآید که جرم متحرکی در یک سیستم در حال ارتعاش یا چرخش، تحت تأثیر نیروی اینرسی خاصی قرار گیرد. قبلا در مقاله ی “فلومتر کوریولیس چگونه کار می کند؟” به بررسی جامع مکانیسم عملکرد فلومتر کوریولیس، بهعنوان دقیقترین فلومتر صنعتی، پرداخته ایم.
در این مقاله، با نگاهی علمی و تحلیلی، به تئوری کار فلومتر کوریولیس پرداخته میشود و معادلات فلومتر کوریولیس در بستر دینامیک سیالات و ارتعاشات بررسی خواهند شد. همچنین ساختار فیزیکی دستگاه، بهویژه در پیکربندی متداول U شکل، به همراه تحلیل فاز، گشتاور پیچشی و ویژگیهای طراحی آن مورد تحلیل قرار میگیرد.
ساختار و اجزای اصلی فلومتر کوریولیس
فلومترهای کوریولیس شامل دو بخش اصلی هستند که هرکدام نقش مهمی در تولید ارتعاش، اندازهگیری سیگنال و تحلیل دبی دارند. در این بخش، این اجزا را بهصورت دقیق بررسی میکنیم.
الف) عناصر اولیه:
- لولههای انتقال سیال: این لولهها معمولاً بهصورت U شکل یا خمیده طراحی میشوند و در دو انتها مهار شدهاند. امکان ارتعاش آزاد آنها در بازه خاصی فراهم شده است تا نیروی کوریولیس در آنها شکل بگیرد.
- محرک الکترومغناطیسی (Exciter): این عنصر ارتعاش کنترلشدهای را در فرکانس طبیعی لولهها ایجاد میکند که لازمهی عملکرد دقیق فلومتر است.
- سنسورهای الکترومغناطیسی: در نقاط کلیدی لوله قرار گرفتهاند تا تغییرات فاز یا تأخیر زمانی حاصل از عبور جریان را تشخیص دهند.
- مدار فیدبک: یک حلقه کنترلی که فرکانس نوسان را در حالت پایه یا هارمونیکهای خاص تثبیت میکند و شرایط پایداری ارتعاش را حفظ مینماید.
ب) عناصر ثانویه:
- مدار الکترونیکی اندازهگیری اختلاف فاز: این مدار با دقت بالا سیگنالهای حاصل از سنسورها را تحلیل کرده و اختلاف فاز میان نقاط ورودی و خروجی لوله را اندازهگیری میکند. این اختلاف فاز مستقیماً با نرخ جریان جرمی متناسب است و اساس محاسبهی معادلات فلومتر کوریولیس را تشکیل میدهد.
تئوری پایه: چرخش و نیروی کوریولیس
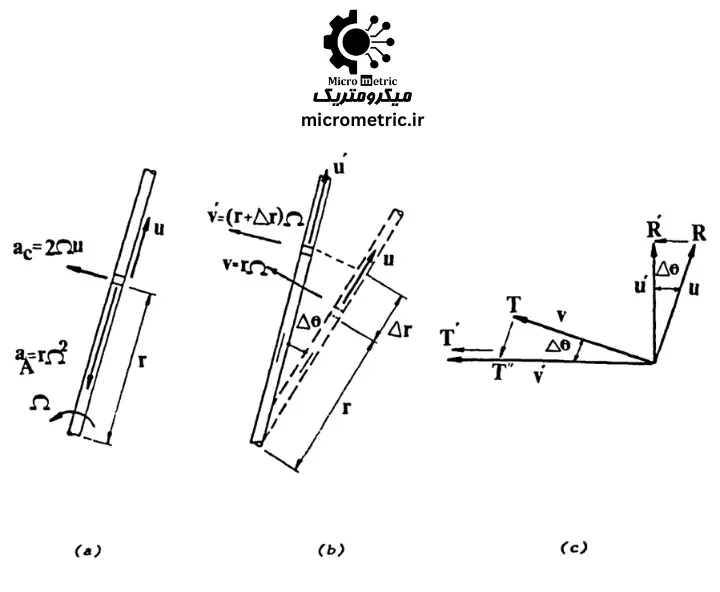
درک نحوهی عملکرد این فلومتر، نیازمند آشنایی با دینامیک دوران و اصول فیزیکی اثر کوریولیس است. در شکل 1-a، مقطعی از یک لوله استوانهای را مشاهده میکنیم که با سرعت زاویهای Ω حول محور z در حال چرخش است. جریان سیال درون این لوله با سرعت متوسط u در راستای محور لوله حرکت میکند.
همزمان، این سیال در معرض دو عامل فیزیکی قرار میگیرد:
- تغییر تکانه زاویهای (angular momentum) به دلیل چرخش لوله
- شتاب گریز از مرکز ناشی از حرکت دورانی
این شرایط باعث میشود که نیروی کوریولیس بر سیال اعمال شود، که شدت آن به سرعت جریان و نرخ چرخش بستگی دارد. بر اساس این پدیده، معادلات حاکم بر فلومتر کوریولیس پایهریزی میشوند که در ادامه مقاله بهطور کامل بررسی خواهند شد.
تحلیل فیزیکی نیروی کوریولیس در معادلات فلومتر کوریولیس
برای درک دقیقتری از شتاب کوریولیس و نحوه شکلگیری آن در ساختار فلومتر، بهتر است رفتار یک المان کوچک از جرم سیال را در دو لحظه متوالی بررسی کنیم. مطابق با شکل 1-b، فرض کنید در زمان \( t \)، سرعت سیال دارای دو مؤلفه \( u \) و \( v \) است. پس از گذشت بازهی زمانی \( \Delta t \)، این مؤلفهها به ترتیب به \( u’ \) و \( v’ \) تغییر مییابند.
برای تجسم تغییرات رخداده در این بازه زمانی، بردارهای سرعت در زمانهای مختلف را از یک مبدأ مشترک ترسیم میکنیم (مطابق با شکل 1-c). در این نمودار برداری، تغییر بردار سرعت کل را میتوان بهصورت مجموع سه بردار تحلیل کرد:
- بردار \( \overrightarrow{TT”} \): بیانگر تغییر سرعت در جهت انتقال خطی
- بردار \( \overrightarrow{RR’} \): نماینده تغییر ناشی از چرخش مرجع
- بردار \( \overrightarrow{T”T’} \): ناشی از شتاب جانبی یا کوریولیس
این سه مؤلفه برداری در کنار یکدیگر توصیف کاملی از نیروهای اینرسی مؤثر در سیستم را ارائه میدهند و نقش کلیدی در شکلگیری معادلات فلومتر کوریولیس دارند. چنین تحلیلی پایهگذار مدلسازی دینامیکی لولههای ارتعاشی در حضور جریان سیال است و بهویژه در طراحی و کالیبراسیون فلومترهای صنعتی کاربرد دارد.
بیان تحلیلی بردارهای شتاب و شکلگیری شتاب کوریولیس
بردار \( \overrightarrow{TT”} \) نشاندهندهی تغییر جهت مؤلفهی سرعت \( v \) است که منجر به ایجاد شتاب مرکزگرا میشود. این شتاب در حد زمانی \( \Delta t \to 0 \) به صورت زیر قابل محاسبه است:
\[ \lim_{\Delta t \to 0} \frac{TT”}{\Delta t} = \lim_{\Delta t \to 0} \left( v \cdot \frac{\Delta \theta}{\Delta t} \right) = r\Omega^2 \tag{1.1} \]
در این معادله، \( \Omega \) سرعت زاویهای سیستم، و \( r \) شعاع چرخش است.
بردار \( \overrightarrow{RR’} \) بیانگر تغییر جهت مؤلفهی سرعت بر اثر دوران است، و بردار \( \overrightarrow{T”T’} \) نشاندهندهی تغییر در اندازهی مؤلفهی \( v \) سرعت به دلیل وجود سرعت \( u \) در راستای محوری لوله میباشد.
شتاب کوریولیس حاصل اثر ترکیبی سرعت نسبی \( u \) و سرعت زاویهای سیستم \( \Omega \) است و در دستگاه مرجع چرخان به شکل زیر بیان میشود:
\[ \lim_{\Delta t \to 0} \frac{RR’ + T”T’}{\Delta t} = \lim_{\Delta t \to 0} \left( u \cdot \frac{\Delta \theta}{\Delta t} + \Omega \cdot \frac{\Delta r}{\Delta t} \right) = 2\Omega u \tag{1.2} \]
این شتاب همواره عمود بر هر دو بردار \( \Omega \) و \( u \) قرار میگیرد و باعث انحراف مسیر جریان سیال درون لوله میشود؛ انحرافی که مبنای عملکرد فلومتر کوریولیس را تشکیل میدهد.
همچنین باید توجه داشت که این شتاب میتواند از طریق نوسان کنترلشده لوله نیز ایجاد شود. در چنین حالتی، نیروی کوریولیس منجر به تولید شتابی نوسانی با همان فرکانس نوسان اصلی میشود و سیگنالهای اندازهگیریشده توسط سنسورها بر این اساس تحلیل میشوند.
تحلیل دینامیکی فلومتر با لوله U شکل
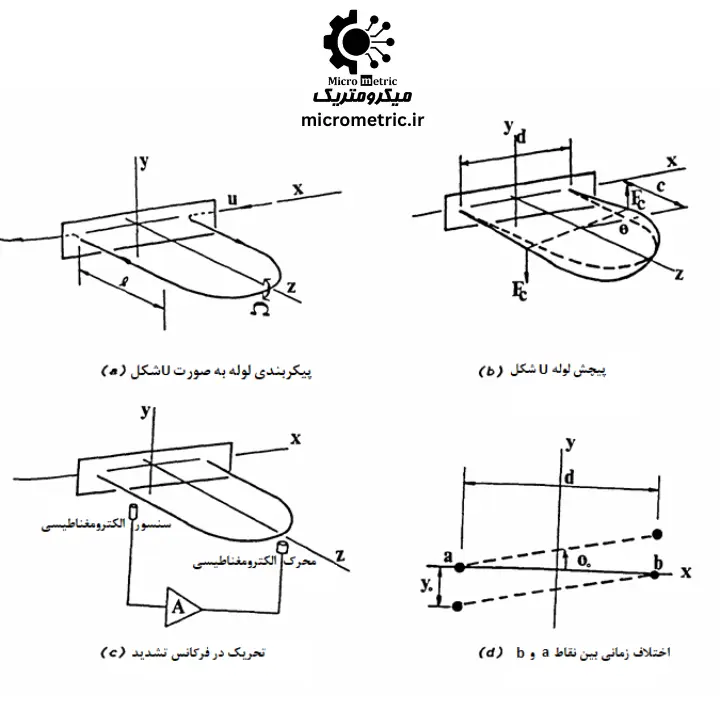
یک فلومتر با پیکربندی لوله بهشکل U را در نظر بگیرید، همانطور که در شکل 2-a نشان داده شده است (سایر پیکربندیها را نیز میتوان بهروشی مشابه تحلیل کرد). در این پیکربندی، محرک الکترومغناطیسی باعث میشود که لوله بهطور تقریبی حول محور x نوسان چرخشی داشته باشد.
سرعت زاویهای این نوسان بهصورت تابع کسینوسی از زمان تعریف میشود:
\[ \Omega = \Omega_0 \cos(\omega t) \tag{1.3} \]
در این حالت، سیال در شاخههای مستقیم لولهی Uشکل در جهتهای مخالف جریان دارد؛ بنابراین، شتاب کوریولیس منجر به پیچش نوسانی لوله حول محور z میشود.
هر ذرهای با جرم \( m \) و سرعت \( \vec{u} \) تحت تأثیر نیروی کوریولیس به صورت زیر قرار میگیرد:
\[ \vec{F}_c = 2m \vec{u} \times \vec{\Omega} \]
این نیرو باعث ایجاد جفت نیروهای \( \pm F_c \) در بخشهای مستقیم لولهی U میشود (شکل 1-b) که مقدار آن بهصورت زیر بیان میشود:
\[ F_c = 2 \rho \Omega_0 \cos(\omega t) \cdot u \cdot l \cdot A \tag{1.4} \]
که در آن:
- \( \rho \): چگالی سیال
- \( l \): طول شاخه مستقیم لوله
- \( A \): سطح مقطع داخلی لوله
- \( u \): سرعت خطی سیال در لوله
این نیروها در حقیقت از اختلاف فشارهای موضعی در راستای عمود بر جریان (راستای y) ناشی میشوند و پایهای برای ایجاد پیچش لوله بهشمار میآیند.
بیان تحلیلی بردارهای شتاب و شکلگیری شتاب کوریولیس
بردار \( \overrightarrow{TT”} \) نشاندهندهی تغییر جهت مؤلفهی سرعت \( v \) است که منجر به ایجاد شتاب مرکزگرا میشود. این شتاب در حد زمانی \( \Delta t \to 0 \) به صورت زیر قابل محاسبه است:
\[ \lim_{\Delta t \to 0} \frac{TT”}{\Delta t} = \lim_{\Delta t \to 0} \left( v \cdot \frac{\Delta \theta}{\Delta t} \right) = r\Omega^2 \tag{1.1} \]
در این معادله، \( \Omega \) سرعت زاویهای سیستم، و \( r \) شعاع چرخش است.
بردار \( \overrightarrow{RR’} \) بیانگر تغییر جهت مؤلفهی سرعت بر اثر دوران است، و بردار \( \overrightarrow{T”T’} \) نشاندهندهی تغییر در اندازهی مؤلفهی \( v \) سرعت به دلیل وجود سرعت \( u \) در راستای محوری لوله میباشد.
شتاب کوریولیس حاصل اثر ترکیبی سرعت نسبی \( u \) و سرعت زاویهای سیستم \( \Omega \) است و در دستگاه مرجع چرخان به شکل زیر بیان میشود:
\[ \lim_{\Delta t \to 0} \frac{RR’ + T”T’}{\Delta t} = \lim_{\Delta t \to 0} \left( u \cdot \frac{\Delta \theta}{\Delta t} + \Omega \cdot \frac{\Delta r}{\Delta t} \right) = 2\Omega u \tag{1.2} \]
این شتاب همواره عمود بر هر دو بردار \( \Omega \) و \( u \) قرار میگیرد و باعث انحراف مسیر جریان سیال درون لوله میشود؛ انحرافی که مبنای عملکرد فلومتر کوریولیس را تشکیل میدهد.
همچنین باید توجه داشت که این شتاب میتواند از طریق نوسان کنترلشده لوله نیز ایجاد شود. در چنین حالتی، نیروی کوریولیس منجر به تولید شتابی نوسانی با همان فرکانس نوسان اصلی میشود و سیگنالهای اندازهگیریشده توسط سنسورها بر این اساس تحلیل میشوند.
استخراج رابطهی دبی جرمی از زاویهی پیچش
معادله (1.9) نشان میدهد که چگونه میتوان دبی جرمی سیال را از طریق اندازهگیری دامنهی پیچش \( \theta_0 \) محاسبه کرد.
انتخاب دقیق فرکانس تحریک نسبت به فرکانس طبیعی مود پیچش بسیار ضروری است، تا نسبت سیگنال به نویز مناسب فراهم شود و امکان اندازهگیری دقیق سیالات با چگالیهای مختلف، بدون نیاز به کالیبراسیون مجدد، فراهم گردد.
بر اساس معادله (1.9)، برای دبی جرمی ثابت، \( \theta_0 \) را میتوان بهصورت زیر بیان کرد:
\[ \theta_0 = \frac{2 \Omega_0 l d}{K \left(1 – \left(\frac{\omega}{\omega_{nt}}\right)^2\right)} \cdot \dot{m} \tag{1.10} \]
در نتیجه، با نزدیک شدن فرکانس تحریک \( \omega \) به فرکانس طبیعی \( \omega_{nt} \)، مقدار \( \theta_0 \) افزایش مییابد. با این حال، میتوان با افزایش طول بازوی گشتاور \( d \) و/یا کاهش سختی پیچشی لوله (کاهش مقدار \( K \)) نیز دامنه پیچش را افزایش داد.
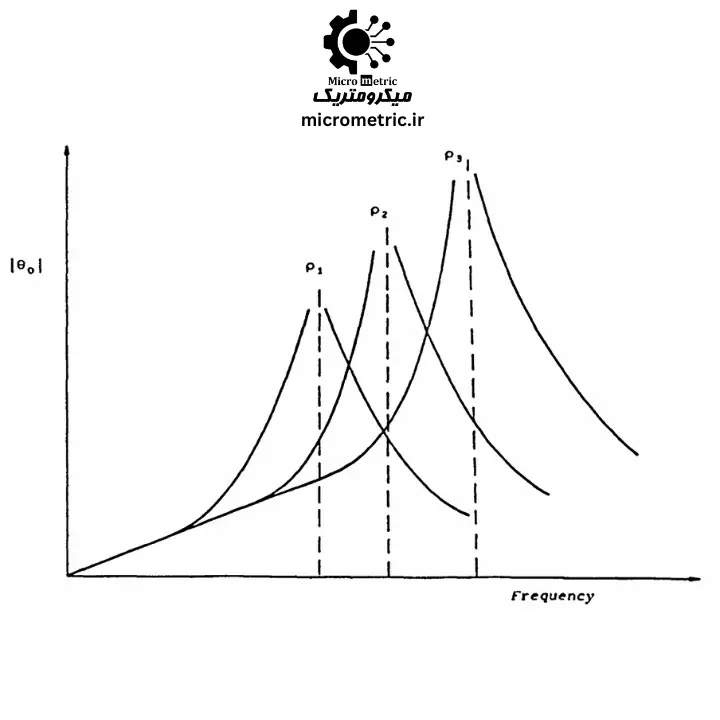
بر اساس معادله (1.10) و مطابق شکل ۳، در فرکانسهای تحریک پایین که \( \omega / \omega_{nt} \ll 1 \)، دامنهی پیچش \( \theta_0 \) بهصورت خطی با \( \Omega_0 \) و \( \dot{m} \) تغییر میکند و به چگالی سیال وابسته نیست.
تأثیر فرکانس تحریک بر زاویهی پیچش
وقتی فرکانس تحریک \( \omega \) به فرکانس طبیعی پیچش \( \omega_{nt} \) نزدیک میشود (یعنی نسبت \( \omega / \omega_{nt} \approx 1 \))، افزایش قابلتوجهی در زاویهی پیچش \( \theta_0 \) مشاهده میشود. این پدیده ناشی از رفتار تشدیدی سیستم ارتعاشی است که موجب افزایش دامنه نوسان میگردد.
اما در حالتی که فرکانس تحریک بسیار بیشتر از فرکانس طبیعی پیچش باشد (یعنی \( \omega \gg \omega_{nt} \))، مقدار \( \theta_0 \) با مجذور فرکانس تحریک رابطه معکوس پیدا میکند و طبق معادله زیر کاهش مییابد:
\[ \theta_0 \propto \frac{1}{\omega^2} \]
این ویژگی، در طراحی و تنظیم فرکانس محرک فلومتر کوریولیس اهمیت ویژهای دارد، زیرا انتخاب نادرست فرکانس میتواند باعث کاهش حساسیت اندازهگیری و افت دقت شود.
وابستگی پیچش به چگالی و فرکانس تحریک
توجه داشته باشید که ممان اینرسی \( I \) به جرم سیستم، و در نتیجه به چگالی سیال وابسته است. بر اساس رابطهی (1.8)، فرکانس طبیعی پیچش \( \omega_{nt} \) نیز بهصورت زیر به چگالی بستگی دارد:
\[ \omega_{nt} = \sqrt{\frac{K}{I}} \tag{1.8} \]
در نتیجه، در شرایطی که دستگاه با فرکانس تحریک ثابتی برابر با \( \omega \) (که به اندازه کافی از \( \omega_{nt} \) فاصله ندارد) و با دامنهی ثابت ارتعاشی \( \Omega_0 \) کار میکند، حساسیت آن به چگالی سیال تغییر خواهد کرد. زیرا افزایش چگالی باعث افزایش \( I \) و کاهش \( \omega_{nt} \) میشود و این تغییر بر نسبت \( \omega / \omega_{nt} \) اثر میگذارد.
برای حل این مشکل در سیالاتی با چگالی متغیر، پیشنهاد میشود لولهها در فرکانس طبیعی پایهی خود، یعنی \( \omega_n \)، ارتعاش داده شوند. این کار با استفاده از مدار فیدبک امکانپذیر است (مطابق شکل 2-c).
از آنجا که فرکانس پایه \( \omega_n \) پایینتر از هارمونیک اول (یعنی \( \omega_{nt} \)) است، نسبت زیر برای طیف وسیعی از چگالیهای سیال تقریباً ثابت باقی میماند:
\[ \frac{\omega}{\omega_{nt}} = \text{constant} \]
بر اساس معادله (1.10)، رابطهی اساسی بین دبی جرمی و پیچش لوله به صورت زیر تعریف میشود:
\[ \theta_0 = \frac{2 \Omega_0 l d}{K(1 – (\omega / \omega_{nt})^2)} \cdot \dot{m} \tag{1.10} \]
این معادله تنها زمانی بهدرستی عمل میکند که دامنهی سرعت زاویهای ارتعاش اصلی \( \Omega_0 \) ثابت باشد. در چنین شرایطی، زاویهی پیچش \( \theta_0 \) مستقیماً با دبی جرمی \( \dot{m} \) متناسب خواهد بود.
اندازهگیری جریان با استفاده از اختلاف زمانی در فلومتر کوریولیس
روش کاربردیتر برای اندازهگیری جریان در فلومتر کوریولیس، استفاده از اختلاف زمانی \( \Delta t \) بین سیگنالهای اندازهگیریشده توسط سنسورهای نوری یا الکترومغناطیسی در دو نقطه، مانند نقاط a و b در شکل 2-b، است.
مختصات \( y \) نقطهی a یا b (در شرایط بدون جریان) بهصورت زیر تعریف میشود:
\[ y = y_0 \sin(\omega t) \]
و در زمان \( t = 0 \)، سرعت برابر است با:
\[ \dot{y}_0 = \omega y_0 \]
در حضور جریان، پیچشی به اندازهی \( \theta_0 \) ایجاد میشود که منجر به اختلاف زمانی جزئی بین عبور نقاط a و b از صفحهی xz میگردد (همانطور که در شکل 2-d نمایش داده شده است). این اختلاف زمان بهصورت زیر بیان میشود:
\[ \Delta t = \frac{\theta_0}{\omega y_0} \tag{1.11} \]
با فرض اینکه \( \theta_0 \ll y_0 \) و با استفاده از معادلات (1.10)، (1.11) و رابطهی زیر:
\[ \dot{y}_0 = \omega y_0 \approx -\Omega_0 c \tag{1.13} \]
رابطه بین دبی جرمی و اختلاف زمانی بهصورت زیر بهدست میآید:
\[ \dot{m} = cK \cdot \frac{1 – \left(\frac{\omega}{\omega_{nt}}\right)^2}{2 l d^2} \cdot \Delta t \tag{1.14} \]
بنابراین، دبی جرمی مستقل از دامنهی ارتعاش اصلی بوده و تنها به هندسهی سیستم، سختی پیچشی \( K \) و فرکانسهای \( \omega \) و \( \omega_{nt} \) وابسته است.
نتیجهگیری
فلومترهای کوریولیس با بهرهگیری از اصول شتاب کوریولیس، امکان اندازهگیری مستقیم و دقیق دبی جرمی را فراهم میکنند. در این مقاله نشان داده شد که روش مبتنی بر اندازهگیری اختلاف زمانی بین دو نقطه از لوله، وابستگی به دامنهی ارتعاش اصلی را حذف میکند.
بنابراین، دبی جرمی مستقل از دامنهی ارتعاش اصلی بوده و تنها به هندسهی سیستم، سختی پیچشی \( K \) و فرکانسهای \( \omega \) و \( \omega_{nt} \) وابسته است.
این ویژگی، عملکرد پایدار فلومتر را در برابر تغییرات محیطی تضمین کرده و آن را به گزینهای ایدهآل برای کاربردهای صنعتی حساس تبدیل میکند.
اگر علاقهمند به مشاهده و خرید فلومتر کوریولیس هستید، وارد فروشگاه محصولات ما شوید:
مشاهده فروشگاه میکرومتریکمنبع برای مطالعه بیشتر:
برای مطالعه بیشتر در مورد تئوری کار فلومتر کوریولیس و تحلیل دینامیکی عملکرد آن و معادلات حاکم بر فلومتر کورولیس می توانید به مقاله ی Theoretical and experimental studies of the Coriolis mass flowmeter – G Sultan – 1990 مراجعه کنید.
– dspace.lib.cranfield.ac.ukمراجعه کنید.
???? برای اطلاعات بیشتر و مشاورهی فنی، با تیم میکرومتریک تماس بگیرید:
- تلفن: ۰۴۱۳۴۲۶۰۰۱۳
- ایمیلmailto:info@micrometric.ir


بدون دیدگاه